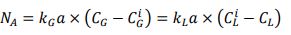Definición de los coeficientes locales de transferencia de masa
gas-líquido (kL y kG)
La operación de transferencia de
masa representada por la figura 5; en ella el punto P
hace referencia a las concentraciones iniciales de contaminante en la fase
gaseosa (CG) y en la fase líquida (CL) y el punto I a las concentraciones en la interfase (CL i y CG i ), donde según postularon Lewis y
Whitman existe un equilibro regido por la ley de Henry.
 |
| Figura 4 Transferencia de masa de contaminante gas-líquido. |
El cálculo de los coeficientes de
transferencia de masa se prefiere en función de números adimensionales. En
ingeniería de reactores heterogéneos, considerando l0 y v0 la longitud y
velocidad característica del sistema, los más comunes son:
El número de Reynolds
El número de Schmidt
El número de Sherwood
Debido a que la interfase es tan
delgada, en ella no hay acumulación de masa de contaminante; de tal manera que
la velocidad con la cual el contaminante abandona la fase gaseosa es igual a la
velocidad con la cual ingresa en la fase líquida. En este caso la velocidad de
transferencia de masa es proporcional a las fuerzas motrices que se presentan
en cada una de las fases; así se obtiene que para la transferencia de masa del
contaminante A:
Donde NA es el flux de
transferencia de masa que puede ser expresado en g.l-1 .s-1
y a es el área interfacial específica en m2 .m-3 . Para
eliminar la proporcionalidad se incorporan en la ecuación los coeficientes
locales de transferencia de masa de la película gaseosa kG y
de la película líquida kL; haciendo un análisis dimensional se pude inferir
que estos coeficientes se expresan usualmente en unidades de m.s -1
.
reorganizando la ecuación
anterior se obtiene la siguiente expresión:
Esta ecuación relaciona a los
coeficientes locales de transferencia de masa y representa la pendiente de la
recta P-I que se muestra en la figura 5.
Se han desarrollado ecuaciones
empíricas para determinar los coeficientes de transferencia
de masa locales en operaciones de
transferencia de masa. La tabla 5, resume las ecuaciones
empíricas más utilizadas para
columnas empacadas aleatoriamente.
 |
| Tabla 2. Ecuaciones empíricas para determinar los coeficientes locales de transferencia de masa en columnas empacadas |
Definición de los coeficientes globales de transferencia de masa
gas-líquido (KGa y
KLa)
Debido a que las concentraciones
en la interfase CL i y CG i no
se pueden determinar fácilmente y prácticamente es imposible; es necesario
desarrollar un modelo que relacione las concentraciones en las fases (CL y CG) que se muestran la figura 4; estas concentraciones son
fácilmente medibles a partir de equipos de medición convencionales.
 |
| Figura 5 Diferencias globales de concentración |
La figura 6 también representa la
transferencia de masa mostrada en la figura 4. En ella, si a partir del punto P
se traza una línea recta paralela al eje y hasta la curva de equilibrio se
obtiene el punto a de coordenadas (CL, CG*); donde CG* es la concentración de
contaminante en el gas que está en equilibrio con la concentración en el
líquido CL. De igual manera si a partir del punto P se traza una línea
recta paralela al eje x hasta la curva de equilibrio se obtiene el punto b de
coordenadas (CL*, CG); en este caso, CL*es la concentración de
contaminante en el líquido que está en equilibrio con CG. Puesto que la curva
de equilibrio es única a una presión y temperatura dadas, CG* en
el equilibrio con CL es una medida adecuada de CG (Treybal et al., 1980);
en este sentido, se obtiene que el flux de transferencia de masa es igual a:

Donde KG es el coeficiente
global de transferencia de masa para la fase gaseosa que puede expresarse en
m.s -1 o m.h -1 . Debido a que las concentraciones en el
punto a se encuentran en equilibrio, se puede utilizar la ley de Henry para
relacionarlas con la concentración real en el sistema:
reemplazando se obtiene que:
De manera análoga el flux de
transferencia de masa NA puede expresarse en función de las concentraciones
en la fase líquida entre los puntos P y b,
así se obtiene:
Donde KL es el coeficiente
global de transferencia de masa para la fase líquida que puede ser expresado en
unidades de m.s -1 o m.h -1 . Las concentraciones en el
punto b que se encuentran sobre la curva de equilibrio también se pueden
relacionar de acuerdo a la ley de Henry:
finalmente se obtiene que:
El área interfacial específica a es muy difícil de determinar
experimentalmente puesto que la interfase gas-líquido no se puede visualizar;
en este sentido, los estudios de transferencia de masa por medio de la
valoración experimental de los coeficientes globales de transferencia de masa
expresan este coeficiente como KLa cuyas unidades de medida generalmente se
expresan en s -1 o h -1 . La tabla 6 resume algunos modelos
desarrollados en estudios de transferencia de masa que se han realizado en BTFs mediante la cuantificación
experimental de los coeficientes de transferencia de masa globales a partir de
balances de materia y datos experimentales de concentraciones.
 |
Tabla 6.Modelos desarrollados para determinar los coeficientes globales de transferencia en BTFs de manera experimental
|